Continuous Additive Algebras and Injective Simulations of Synchronization Trees

The (in)equational properties of the least fixed point operation on (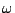 $\omega$ -)continuous functions on ( 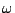$\omega$ -)complete partially ordered sets are captured by the axioms of (ordered) iteration algebras, or iteration theories. We show that the inequational laws of the sum operation in conjunction with the least fixed point operation in continuous additive algebras have a finite axiomatization over the inequations of ordered iteration algebras. As a byproduct of this relative axiomatizability result, we obtain complete infinite inequational and finite implicational axiomatizations. Along the way of proving these results, we give a concrete description of the free algebras in the corresponding variety of ordered iteration algebras. This description uses injective simulations of regular synchronization trees. Thus, our axioms are also sound and complete for the injective simulation (resource bounded simulation) of (regular) processes

Abstract: