Abstract:
Given a collection of connected components, it is often desired
to cluster together parts of strong correspondence, yielding a hierarchical
structure. We address the automation of this process and apply heuristics to
battle the combinatorial and computational complexity. We define a cost
function that captures the quality of a structure relative to the connections
and favors shallow structures with a low degree of branching. Finding a
structure with minimal cost is shown to be 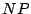 -complete. We present a greedy
polynomial-time algorithm that creates an approximative good solution
incrementally by local evaluation of a heuristic function. We compare some
simple heuristic functions and argue for one based on four criteria: The
number of enclosed connections, the number of components, the number of
touched connections and the depth of the structure. We report on an
application in the context of formal verification, where our algorithm serves
as a preprocessor for a temporal scaling technique, called ``Next''
heuristic. The latter is applicable in enumerative reachability analysis and
is included in the recent version of the MOCHA model checking tool. We
demonstrate performance and benefits of our method and use an asynchronous
parity computer, a standard leader election algorithm, and an opinion poll
protocol as case studies
-complete. We present a greedy
polynomial-time algorithm that creates an approximative good solution
incrementally by local evaluation of a heuristic function. We compare some
simple heuristic functions and argue for one based on four criteria: The
number of enclosed connections, the number of components, the number of
touched connections and the depth of the structure. We report on an
application in the context of formal verification, where our algorithm serves
as a preprocessor for a temporal scaling technique, called ``Next''
heuristic. The latter is applicable in enumerative reachability analysis and
is included in the recent version of the MOCHA model checking tool. We
demonstrate performance and benefits of our method and use an asynchronous
parity computer, a standard leader election algorithm, and an opinion poll
protocol as case studies
Available as PostScript, PDF.