Abstract:
Recently, Coquand and Palmgren considered systems of
intuitionistic arithmetic in all finite types together with various forms of
the axiom of choice and a numerical omniscience schema (NOS) which
implies classical logic for arithmetical formulas. Feferman subsequently
observed that the proof theoretic strength of such systems can be determined
by functional interpretation based on a non-constructive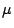 
-operator and
his well-known results on the strength of this operator from the 70's.
In this note we consider a weaker form LNOS (lesser numerical omniscience schema) of NOS which suffices to derive the strong form of binary König's lemma studied by Coquand/Palmgren and gives rise to a new and mathematically strong semi-classical system which, nevertheless, can proof theoretically be reduced to primitive recursive arithmetic PRA. The proof of this fact relies on functional interpretation and a majorization technique developed in a previous paper.
-operator and
his well-known results on the strength of this operator from the 70's.
In this note we consider a weaker form LNOS (lesser numerical omniscience schema) of NOS which suffices to derive the strong form of binary König's lemma studied by Coquand/Palmgren and gives rise to a new and mathematically strong semi-classical system which, nevertheless, can proof theoretically be reduced to primitive recursive arithmetic PRA. The proof of this fact relies on functional interpretation and a majorization technique developed in a previous paper.
Available as PostScript, PDF, DVI.