Introduction to ALF - an Interactive Proof Editor
Introduction to ALF - an Interactive Proof Editor
Lena Magnusson
In 6th
NWPT, page 269
Abstract:
We will give a description of incremental type checking, which
is the main tool for doing interactive proof development in ALF.ALF
is based on Martin-Löf's type theory, which is a logical framework in the
sense that the language can be extended with new definitions. The language is
a functional language with dependent function types, which can be extended
with data types, functions and constants as new definitions, in the spirit of
traditional functional languages. The dependent function type gives us a
richer type system, in which propositions and specifications of programs can
be represented. Thus, the relation  can denote a program
can denote a program  of type
of type
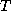 or a proof
or a proof  of proposition
of proposition 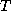 . This relation is decidable and the
type (proof) checking algorithm is the core of the proof editor ALF. However,
the objective of ALF is to interactively build proof terms or programs, in a
flexible and safe way. For this purpose we have extended the language with
the notion of placeholders (meta variables) which denotes sub-terms intended
to be filled in. Hence, an incomplete proof term is a term containing
placeholders, and proof refinement corresponds to successively replacing a
placeholder by a (possibly incomplete) sub-term.
. This relation is decidable and the
type (proof) checking algorithm is the core of the proof editor ALF. However,
the objective of ALF is to interactively build proof terms or programs, in a
flexible and safe way. For this purpose we have extended the language with
the notion of placeholders (meta variables) which denotes sub-terms intended
to be filled in. Hence, an incomplete proof term is a term containing
placeholders, and proof refinement corresponds to successively replacing a
placeholder by a (possibly incomplete) sub-term.
The type checking
algorithm is extended to handle incomplete terms which gives as result a
unification problem, i.e. a set of equations and typing restrictions of the
placeholders occurring in the incomplete term. This set corresponds to the
requirements which must be satisfied in future refinements. The unification
problem can not always be solved, due to higher order placeholders, and
unsolved equations are left as constraints restricting future instantiations
of the placeholders. Correctness of a refinement is established by type
checking the refined (incomplete) proof term. Thus, proof refinement is
reduced to type checking incomplete proof terms.
Comments
Chalmers Technical University, Inst. for Computer Science,
Göteborg, Sweden. E-mail: lena@cs.chalmers.se.
Available as PostScript,
DVI.
![[BRICS symbol]](http://www.daimi.aau.dk/BRICS/GIF/BRICS/msymbol8mm.GIF) BRICS WWW home page
BRICS WWW home page
 can denote a program
can denote a program  of type
of type
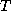 or a proof
or a proof  of proposition
of proposition 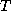 . This relation is decidable and the
type (proof) checking algorithm is the core of the proof editor ALF. However,
the objective of ALF is to interactively build proof terms or programs, in a
flexible and safe way. For this purpose we have extended the language with
the notion of placeholders (meta variables) which denotes sub-terms intended
to be filled in. Hence, an incomplete proof term is a term containing
placeholders, and proof refinement corresponds to successively replacing a
placeholder by a (possibly incomplete) sub-term.
. This relation is decidable and the
type (proof) checking algorithm is the core of the proof editor ALF. However,
the objective of ALF is to interactively build proof terms or programs, in a
flexible and safe way. For this purpose we have extended the language with
the notion of placeholders (meta variables) which denotes sub-terms intended
to be filled in. Hence, an incomplete proof term is a term containing
placeholders, and proof refinement corresponds to successively replacing a
placeholder by a (possibly incomplete) sub-term.