Boolean automata are compact representations of synchronous
reactive systems. The compactness manifests in avoiding the well-known
``state explosion'' problem which arises from representing parallel
composition by a standard product construction.In the computational
model for synchronous reactive systems, time is assumed to be discrete, i.e. divided into enumerable number of non-overlapping
segments, called instances of time. In every instance of time, a
synchronous reactive system performs a so-called reaction step, which
consists in fetching inputs, computing, and emitting outputs. The
fetch-compute-emit sequence is considered to be an atomic action which takes
exactly one instance of time. A system may consist of several reactive
components, running in parallel and communicating with each other. The
components perform their reaction steps simultaneously, i.e. in the same
instance of time, and the outputs emitted in one component are immediately
available to all other components. Thus, communication is based on
instantaneous broadcasting, used in the synchronous programming languages
Esterel, Lustre and Argos, as opposed to instantaneous hand-shaking, used in
synchronous CCS.
In fact, we only consider pure synchronous
reactive systems, i.e. those in which all inputs and outputs are pure
signals. A pure signal does not carry a value. It is either present or
absent, in every instance of time.
It is convenient to represent a
pure synchronous reactive system (with signals 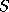 ), by a Mealy
automaton whose transitions are labelled by pairs
), by a Mealy
automaton whose transitions are labelled by pairs 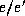 , where
, where 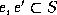 . A transition
. A transition 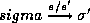 , where
, where
 and
and 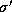 are states, describes a possible reaction step of the
system. It has the following intuitive reading: provided the system starts an
instance in state
are states, describes a possible reaction step of the
system. It has the following intuitive reading: provided the system starts an
instance in state  and
and  is the set of all signals present during
the instance, the system emits signals
is the set of all signals present during
the instance, the system emits signals 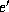 and finishes the instance in
state
and finishes the instance in
state 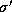 . In such a setting, parallel composition of reactive systems
is represented by a product of Mealy automata, which leads to the well-known
``state explosion'' problem.
. In such a setting, parallel composition of reactive systems
is represented by a product of Mealy automata, which leads to the well-known
``state explosion'' problem.
It turns out that the transition relation
of a pure synchronous reactive system can be coded by two sets of Boolean
functions. The first one represents a set of (possibly recursive) Boolean
equations whose solutions represent pairs 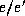 . The second one represents a
set of simultaneous Boolean assignments which represent changes of
states.
. The second one represents a
set of simultaneous Boolean assignments which represent changes of
states.
In the paper, we show how to compose such Boolean automata
using typical operations, like sequential and parallel composition, choice,
iteration and preemption. The main result is that a Boolean automaton grows
linearly with the growth of a reactive synchronous system it
represents.
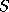 ), by a Mealy
automaton whose transitions are labelled by pairs
), by a Mealy
automaton whose transitions are labelled by pairs 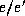 , where
, where 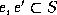 . A transition
. A transition 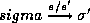 , where
, where
 and
and 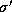 are states, describes a possible reaction step of the
system. It has the following intuitive reading: provided the system starts an
instance in state
are states, describes a possible reaction step of the
system. It has the following intuitive reading: provided the system starts an
instance in state  and
and  is the set of all signals present during
the instance, the system emits signals
is the set of all signals present during
the instance, the system emits signals 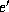 and finishes the instance in
state
and finishes the instance in
state 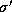 . In such a setting, parallel composition of reactive systems
is represented by a product of Mealy automata, which leads to the well-known
``state explosion'' problem.
. In such a setting, parallel composition of reactive systems
is represented by a product of Mealy automata, which leads to the well-known
``state explosion'' problem.