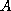 implies
implies
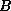 implies
implies 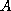 ). Looking at this proposition as a type we see that this is
the type of the
). Looking at this proposition as a type we see that this is
the type of the 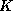 combinator. In type theory we then say that the
combinator. In type theory we then say that the 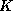 combinator proofs the proposition (
combinator proofs the proposition (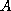 implies
implies 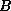 implies
implies 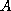 ).
).
Catarina Coquand
In 6th NWPT, page 157
The basic idea behind using type
theory for developing proofs and programs is the Curry-Howard isomorphism
between propositions and types. Take for example the proposition (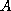 implies
implies
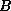 implies
implies 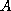 ). Looking at this proposition as a type we see that this is
the type of the
). Looking at this proposition as a type we see that this is
the type of the 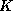 combinator. In type theory we then say that the
combinator. In type theory we then say that the 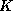 combinator proofs the proposition (
combinator proofs the proposition (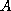 implies
implies 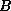 implies
implies 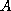 ).
).
The language that is used is a functional language with dependent types. Hence programs and proofs can be described in the same language. We use inductive definitions for our specifications. Introduction rules in logic corresponds to defining a type by its constructors. Proofs are functions defined by pattern matching over these types. We shall also mention how this can be extended to proofs about infinite objects.
Comments
Chalmers Technical University, Inst. for Computer Science,
Göteborg, Sweden. E-mail: catarina@cs.chalmers.se.
Available as PostScript,
DVI.