Abstract:
This dissertation studies the use of methods of proof theory in
extracting new information from proofs in subsystems of classical analysis.
We focus mainly on ineffective proofs, i.e. proofs which make use of
ineffective principles ranging from weak König's lemma to full
comprehension. The main contributions of the dissertation can be divided into
four parts:
- A discussion of how monotone functional interpretation provides the right notion of ``numerical implication'' in analysis. We show among other things that monotone functional interpretation naturally creates well-studied moduli when applied to various classes of statements (e.g. uniqueness, convexity, contractivity, continuity and monotonicity) and that the interpretation of implications between those statements corresponds to translations between the different moduli.
- A
case study in
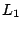 -approximation, in which we analyze Cheney's proof of
Jackson's theorem, concerning uniqueness of the best approximation, w.r.t.
-approximation, in which we analyze Cheney's proof of
Jackson's theorem, concerning uniqueness of the best approximation, w.r.t. 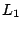 -norm, of continuous functions
-norm, of continuous functions ![$f \in C[0, 1]$](Abs/img2.gif) by polynomials of bounded
degree. The result of our analysis provides the first effective modulus of
uniqueness for
by polynomials of bounded
degree. The result of our analysis provides the first effective modulus of
uniqueness for 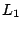 -approximation. Moreover, using this modulus we give the
first complexity analysis of the sequence of best
-approximation. Moreover, using this modulus we give the
first complexity analysis of the sequence of best 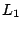 -approximations for
polynomial-time computable functions
-approximations for
polynomial-time computable functions ![$f \in C[0, 1]$](Abs/img2.gif) .
.
- A comparison between three different forms of bar recursion, in which we show among other things that the type structure of strongly majorizable functionals is a model of modified bar recursion, that modified bar recursion is not S1-S9 computable over the type structure of total continuous functions and that modified bar recursion de nes (primitive recursively, in the sense of Kleene) Spector's bar recursion.
- An adaptation of functional interpretation to
handle ine ective proofs in feasible analysis, which provides the first
modular procedure for extracting polynomial-time realizers from ineffective
proofs (i.e. proofs involving weak König's lemma) of
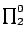 -theorems in feasible analysis.
-theorems in feasible analysis.
Available as PostScript, PDF.